Начертательная геометрия – одна из учебных дисциплин,
составляющих основу инженерного образования, она излагает методы,
которые применяются при составлении и чтении чертежей.
В курсе начертательной геометрии рассматриваются следующие
основные вопросы:
1) построение изображений пространственных форм на плоскости,
т.е. составление чертежей;
2) решение геометрических задач в пространстве при помощи
чертежей на плоскости, т.е. чтение чертежей.
Следовательно, в начертательной геометрии свойства предметов
изучаются непосредственно по чертежу. Для того, чтобы чертеж был
геометрически равноценным изображаемому предмету (оригиналу)
он должен отвечать следующим требованиям:
1) чертеж должен быть наглядным;
2) чертеж должен быть обратимым, т.е. таким, чтобы по нему можно
было точно воспроизвести форму и размеры изображаемого предмета;
3) чертеж должен быть достаточно простым для графического выполнения.
В курсе начертательной геометрии студент получает навык
построения линий и фигур, а также их проекций.
Определение натуральных величин, взаимное пересечение
плоскостей и геометрических тел, методы решения практических
задач по построению и определению истинных размеров
рассматривает курс начертательной геометрии.
Практический пример построения Овала для изображения
в аксонометрии отверстия диаметром 100мм.
Как начертить овал быстро - Рассмотрим несколько простейших задач курса Начертательной геометрии. 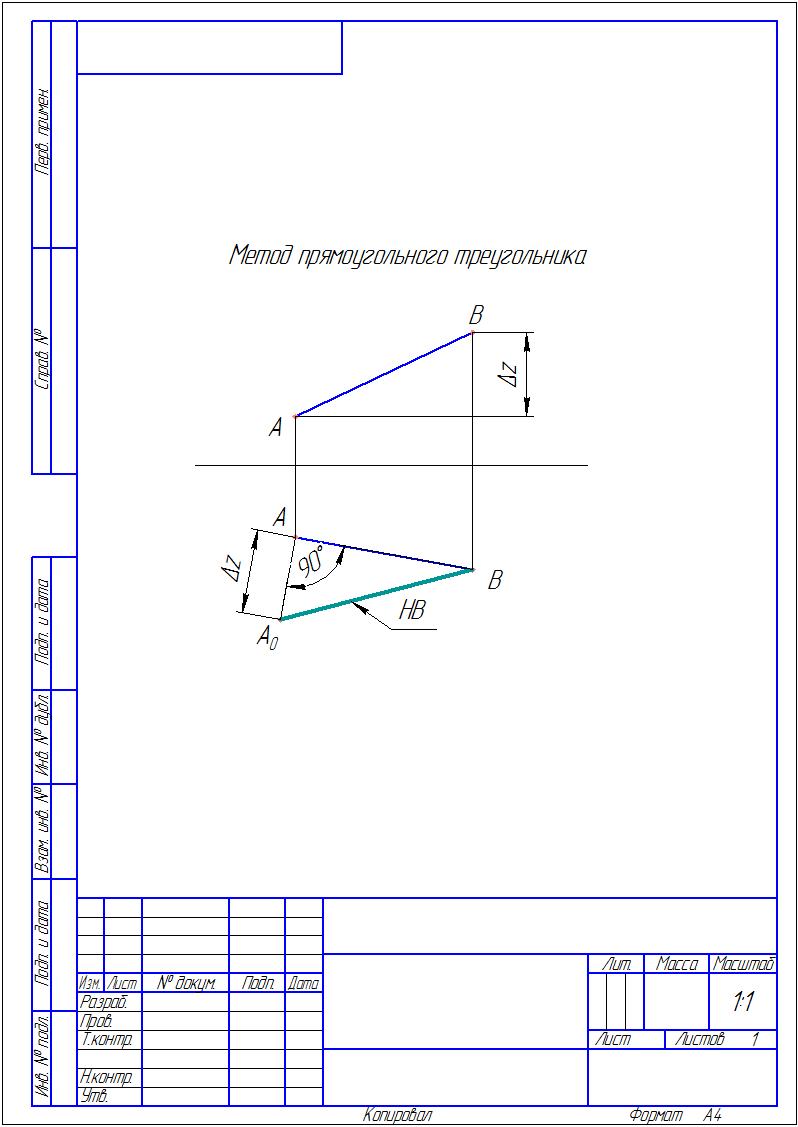Натуральная величина отрезка -
если даны две проекции отрезка,
замерив высоту между его точками
(дельта z) и отложив её в другой
проекции под прямым углом к отрезку,
получим точку А0, соединив которую
с точкой B найдём натуральную величину
отрезка АВ, которая равна длине А0В.
Данный способ определения натуральной
величины называется методом
прямоугольного треугольника
Построим плоскость на расстоянии 40 мм от заданной.
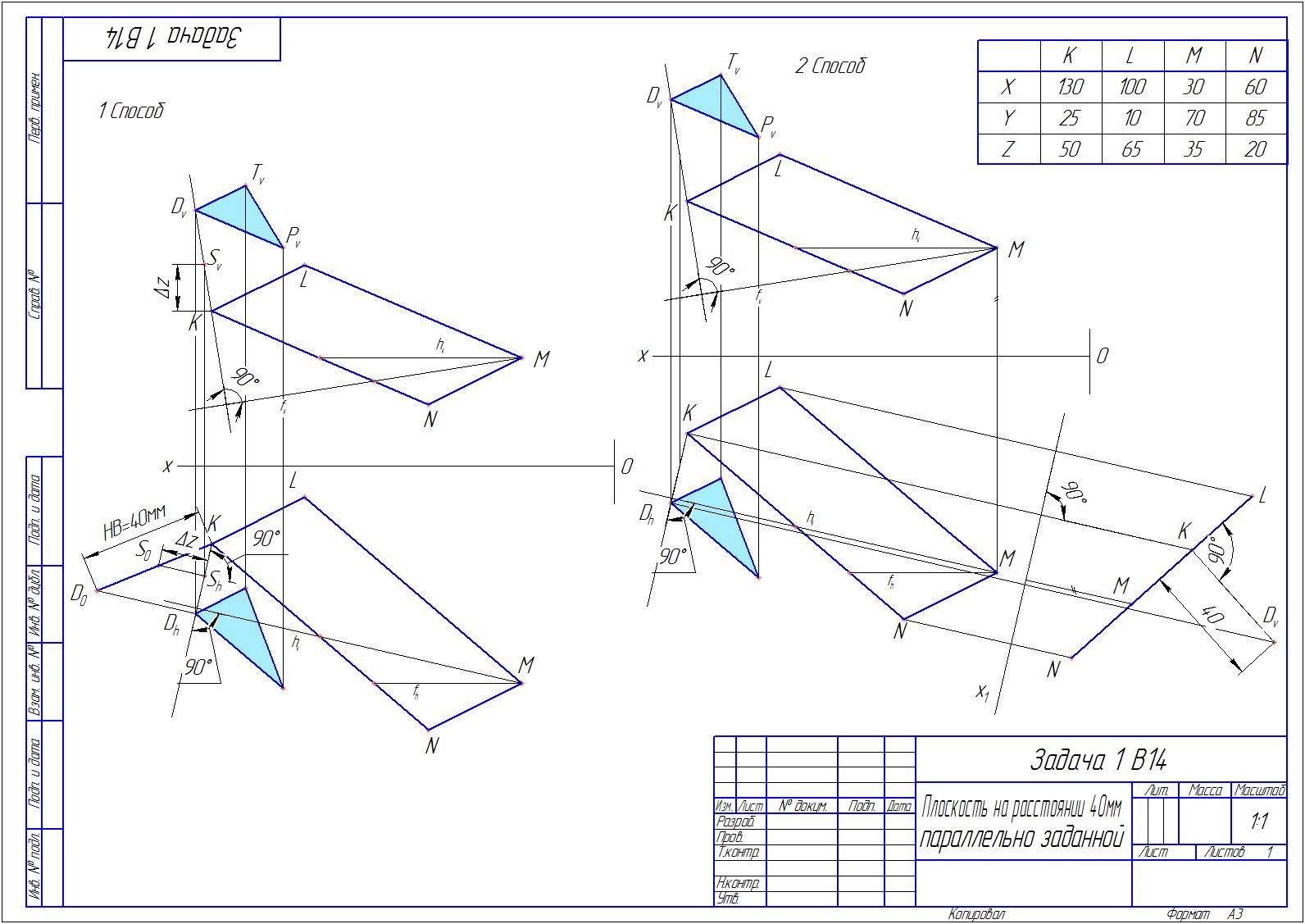
Решим данную задачу двумя способами. 1 Способ.
Для параллелограмма проведём в плоскости П2 горизонталь h и спроецируем её в плоскость П1. Далее в горизонтальной плоскости построим фронталь f и спроецируем её на П2. Опустим перпендикуляры на h и f из точки К.
На данных перпендикулярах отметим произвольную точку S. Из точки S1 отложим перпендикуляр длиной дельта z,
в результате получим точку S0 которая по методу прямоугольного треугольника даст нам направление линии натуральных величин. Остаётся отложить в данном направлении 40 мм и подученную точку Д0 вернуть на перпендикуляр к горизонтали и спроецировать в плоскость П2. Чтобы через точку Д провести плоскость параллельную заданной - мы зададим плоскость двумя пересекающимися прямыми которые начертим параллельно KL и KN. Готово.
2 Способ (замена плоскостей) -
После проведения горизонтали мы строим новую ось x1 перпендикулярно данной горизонтали h1. Проводим к ней линии связи из каждой точки параллелограмма, где новые точки будут расположены на расстояниях отмеряемых с плоскости П2.
Параллелограмм спроецировался в отрезок и нам осталось отмерить от него 40 мм и отмеченную точку Д перенести в плоскости П1 и П2.
В результате решения получаем ту же плоскость QTP скачать чертёжНайдём линию пересечения двух плоскостей.
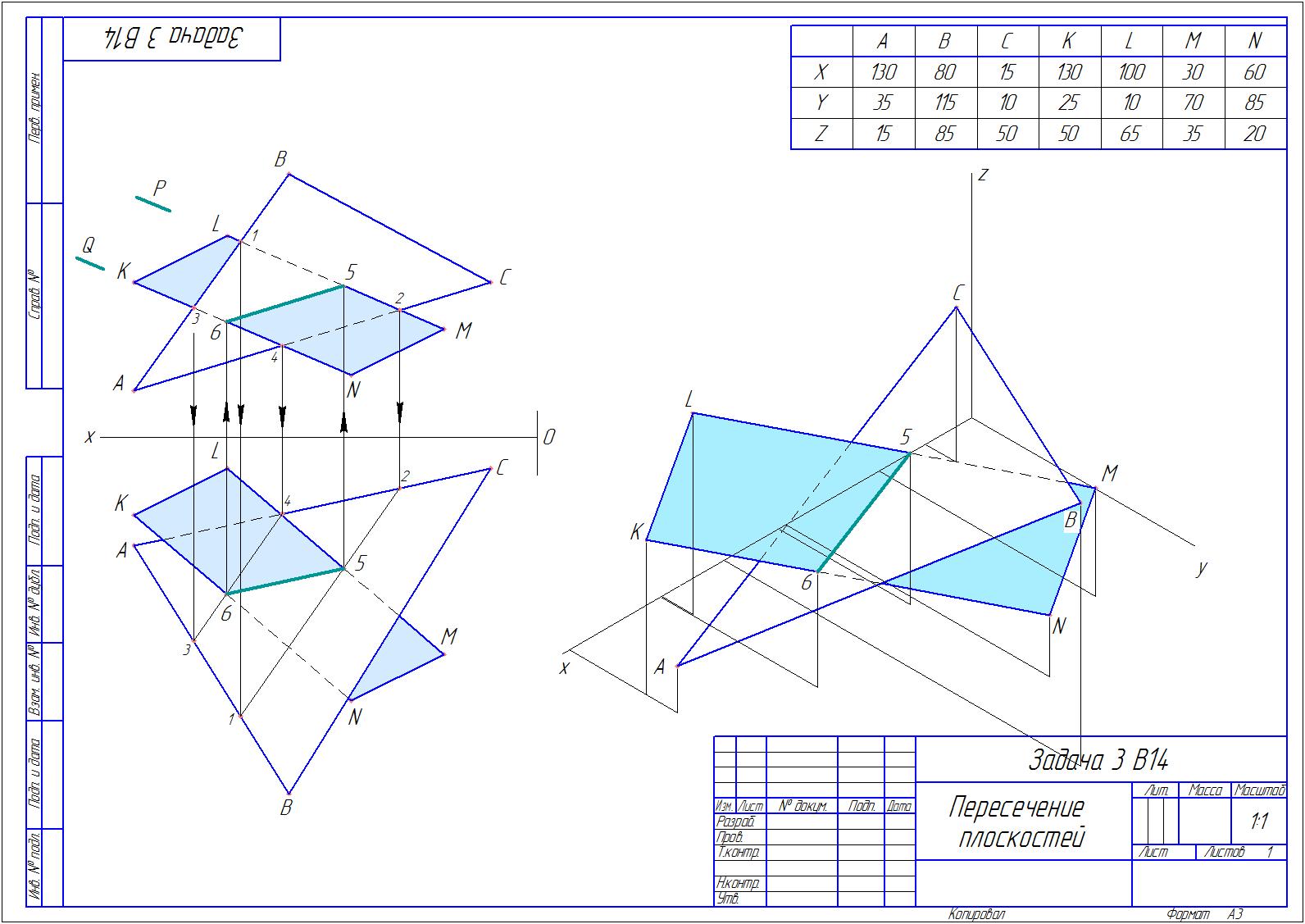
скачать чертёж По заданным координатам точек A,B,C,K,L,M,N строим две плоскости (параллелограмм
и треугольник). Проведём плоскости P и Q через стороны параллелограмма.
Проекция точки 1 находится в плоскости Р(плоскость отрезка LM) и принадлежит стороне АВ.
Проекция точки 2 тоже находится в плоскости Р и принадлежит стороне АС.
Спроецируем точки 1 и 2 на горизонтальную плоскость и соединим их отрезком 1-2.
Отрезок 1-2 пересечёт отрезок LM в точке 5(которая является общей точкой для обеих
плоскостей). Аналогично используя плоскость Q по точкам 3 и 4 находим точку 6
(отрезок 3-4 пересекает KN в точке 6).
Соединив точки 5 и 6 между собой получаем искомую линию пересечения
наших плоскостей.
Чтобы получить наглядное изображение в изометрии (картинка справа)
отмечаем последовательно каждую из точек откладывая x,y,z параллельно
соответствующим осям координат(координаты точек 5 и 6 отмеряем в прямоугольной
системе координат).Найдём линию пересечения двух объёмных поверхностей.
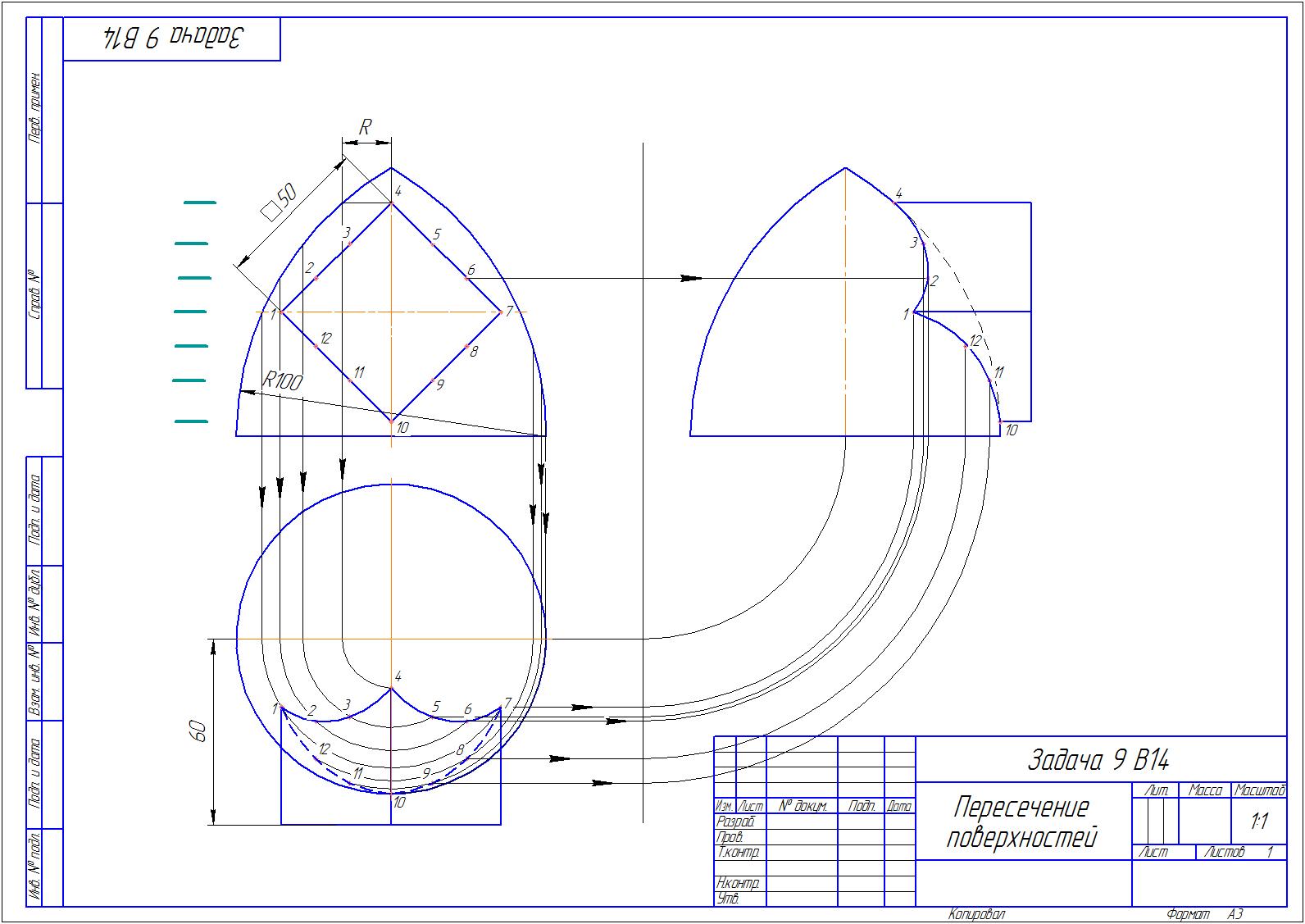
скачать чертёж
На виде спереди четырехугольная призма проецируется в квадрат,
который и будет являться линией пересечения фигур на фронтальной проекции чертежа.
Поделим стороны квадрата произвольно на несколько частей точками 1...12.
Через каждую из точек проведём горизонтальную плоскость. Каждая плоскость
будет пересекать нашу вторую фигуру по окружности, на которой расположены
наши соответствующие точки. Зная это, найдем наши точки на виде сверху.
Так точка 4 находится на окружности радиуса R проведём этот радиус на виде
сверху до пересечения с линией связи от точки 4.
Аналогично находим остальные точки по соответствующим радиусам на линиях связи.
Соединяем пронумерованные полученные точки, учитывая видимость линии пересечения.
Чтобы построить линию пересечения в профильной проекции, достаточно провести для
каждой точки линии связи из П1 и П2 на плоскость П3 до их взаимного пересечения.
Данный ход решения основан на методе сечений.
Для случая если у нас пересекаются два тела вращения (например конус и цилиндр),
используется метод сфер, но это уже другая история...
Линия пересечения методом Сфер. Развёртка.
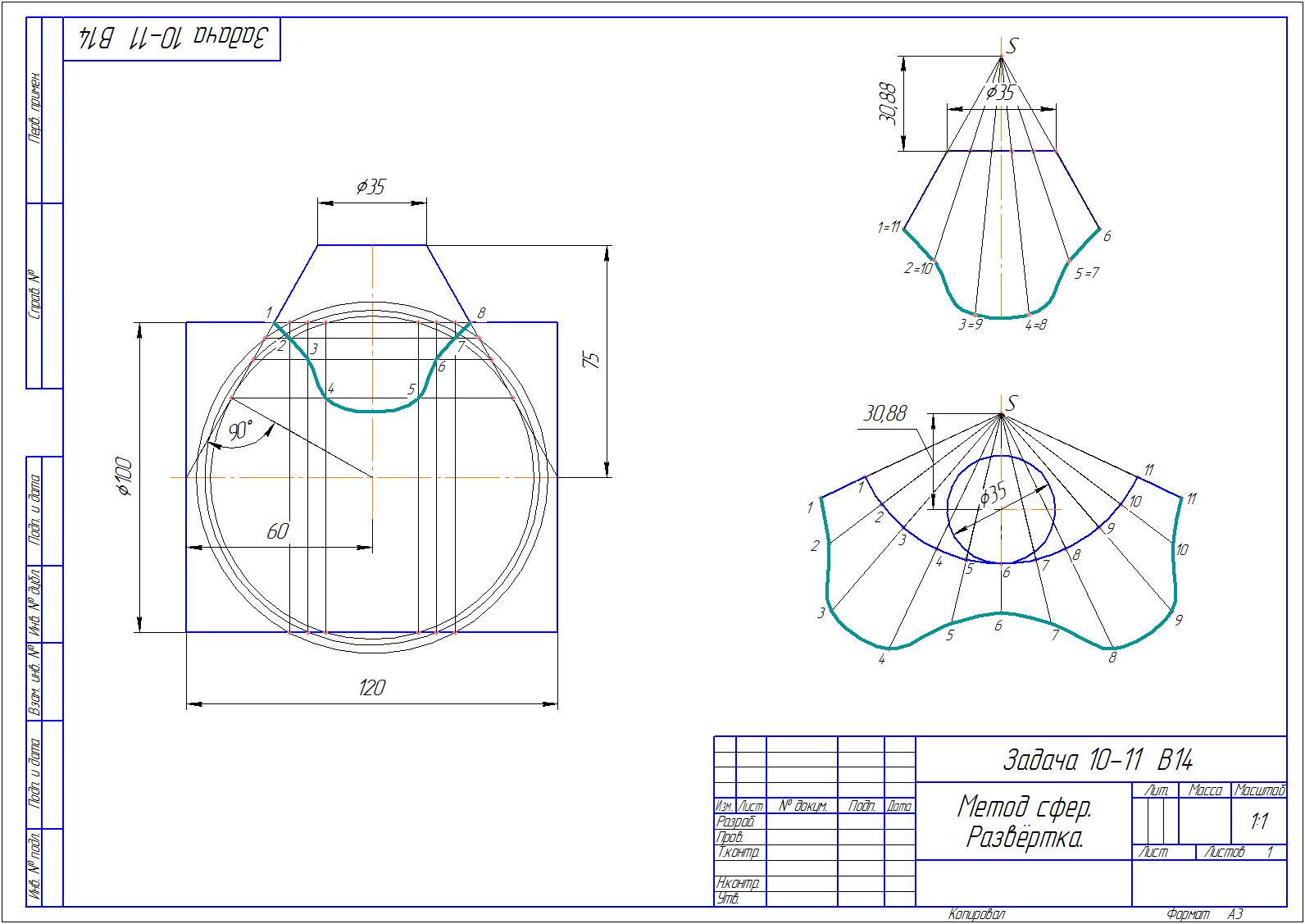
Задачи на пересечение фигур решаются методом сфер если обе пересекающиеся фигуры
- тела вращения и их оси пересекаются. Задача решается поочередным построением нескольких
сфер с увеличением их радиуса. Сферы строятся с центром в точке пересечения осей вращения фигур.
Дано - Цилиндр и Усечённый конус.
Первая сфера имеет радиус окружности вписанной в большую из фигур. Наша первая сфера
имеет радиус окружности, вписанной в конус(показано перпендикуляром из центра сфер
к образующей конуса). Данная окружность пересекает конус в двух точках (касательных) и
пересекает цилиндр в двух точках сверху, и в двух снизу. Отметим получившиеся точки
и соединим их тонкой линией. Три получившиеся отрезка пересекутся между собой в точках
4 и 5 - это и есть наши первые искомые точки линии пересечения. Проведём вторую сферу.
Она также пересечет цилиндр и пересечёт конус. Соединяя получившиеся точки имеем пересечение
отрезков в точках 3 и 6. Третья сфера даёт нам точки 2 и 7.
Точки 1 и 8 отмечаем в пересечении проекций фигур. Соединяя плавной кривой полученные
точки, строим Линию пересечения конуса с цилиндром.
Задача решена.
Аналогичное решение имеют все задачи для тел вращения с пересекающимися осями. Построим развёртку отсеченной части конуса. Для этого найдём его вершину S и поделим
точками верхнее основание на 10 равных частей. Проведём через данные точки отрезки
соединяющие вершину S с линией пересечения. Последовательно пронумеруем точки
на линии пересечения. Строим развертку верхнего основания усеченного конуса и линию
верхней окружности, которую пользуясь формулой длины окружности L=ñ·D разрываем
и делим на 10 равных частей. Нумеруем полученные точки. Остаётся через них
последовательно провести отрезки длины которых берем с верхнего рисунка.S1,S2,S3...
Соединив между собой полученные концы данных отрезков имеем развёртку
нашего усечённого конуса.
Сфера с вырезом.
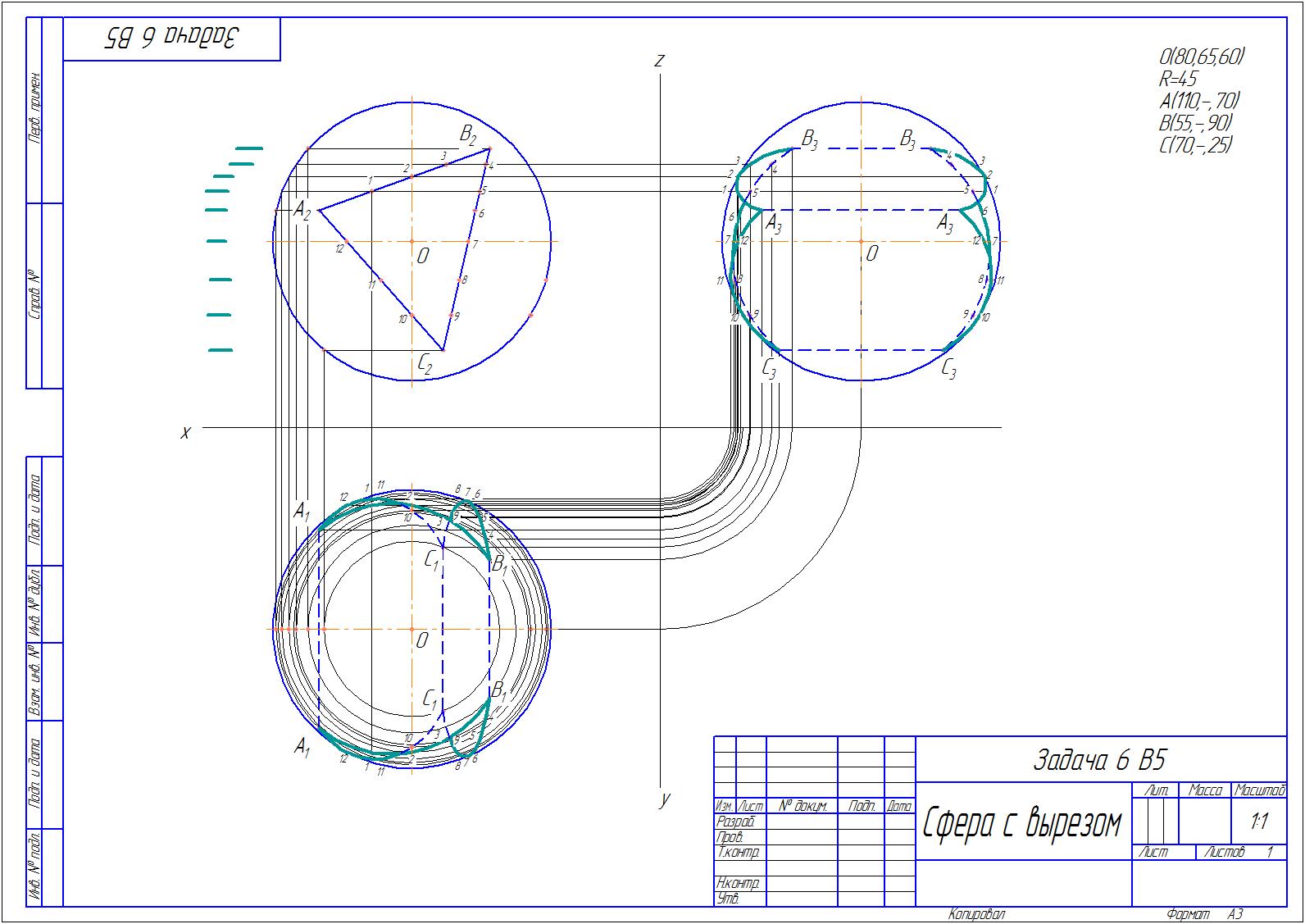
Дано - радиус и центр сферы, даны координаты трёх точек образующих вырез в сфере
в виде треугольной призмы. Построить линию выреза.
На фронтальной проекции линия выреза сформирована в виде треугольника, расположенного
параллельно фронтальной плоскости. Разбиваем данную линию на несколько промежуточных точек,
достаточных для построения линии выреза. Через каждую из точек проводим горизонтальную
секущую плоскость. Данные плоскости отсекают на виде сверху сферу по окружностям.
Радиус каждой окружности мы можем измерить на главном виде и перенести на вид сверху.
Данная окружность пересечёт вертикальную линию связи от нужной точки в двух искомых точках.
Последовательно производя такие действия для каждой точки находим линию пересечения
на виде сверху. Соединяем точки плавной кривой.По взаимному расположению точек
относительно оси сферы определяем видимость полученных линий.
Для получения линии выреза на фронтальном виде достаточно определить пересечения
линий связи с проекций П1 и П2 последовательно для каждой точки. Видимость линии
на виде слева определяется аналогично предыдущей.
Сечение конуса плоскостью общего положения.
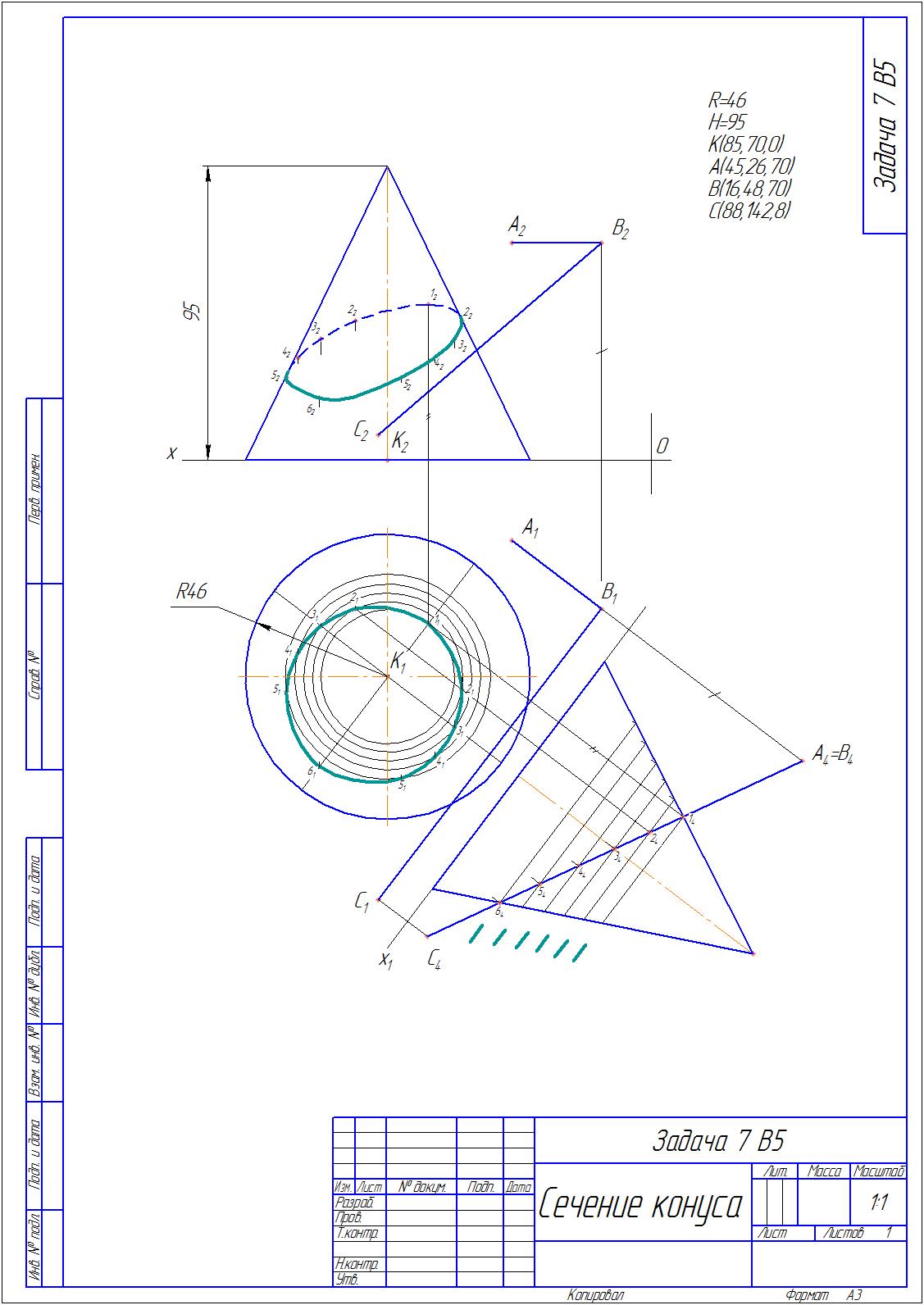
Дано - высота и радиус конуса, а также три точки задающие плоскость общего положения
пересекающую конус.Нужно определить линию пересечения плоскостью.
На первом этапе видим что АВ - отрезок задающий плоскость расположен горизонтально,
следовательно является горизонталью.
Проведём методом замены плоскостей новую ось Х1 перпендикулярно отрезку АВ,
тем самым наша плоскость развернётся в отрезок.
Произведем построения плоскости и конуса в новой плоскости П4, координаты каждой точки
для построения берутся по высоте точки в плоскости П2.
В плоскости П4 линию сечения конуса разбиваем несколькими промежуточными точками,
через каждую из которых проводим секущую плоскость параллельно оси Х2.
Каждая секущая плоскость пересекает конус по окружности. Поочередно переносим каждую
из точек из плоскости П4 в плоскость П1 отмечая точки на пересечении секущей окружности
с линией связи. Соединяем полученные точки плавной кривой.
Теперь для каждой из точек в плоскости П1 проведём линии связи в плоскость П2.
Высота каждой новой точки в плоскости П2(координата z) отмеряется в плоскости П4.
Второй способ нахождения точек - через образующие конуса.
Привёл примеры основных задач.
Кому непонятно письменное решение - обращайтесь лично для репетиторства .
Меня найдёте в колонке справа - КОНТАКТЫ или на почту adv19721@ya.ru
========================================================= Поделись с другом
